[백준 15685] 드래곤 커브

[문제 바로가기]

15685번: 드래곤 커브

 

💡풀이💡

문제에서 나온 정보 정리!

 

좌표 평면의 방향

익숙하게 사용하는 좌표 평면의 방향은 x축➡ y축 ⬆이지만 문제에서는 y축이 ⬇ 방향으로 되어 있음

>> 90도 회전할 때 방향에 주의!

 

🐲드래곤 커브 그리기🐲

문제에서 설명하고 있는 드래곤 커브를 그리는 규칙을 정리 해보면 이렇게 볼 수 있다.

1세대 ➡ 2세대

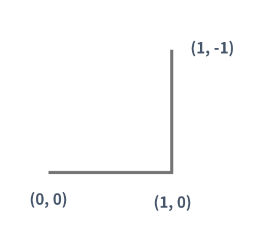
0세대 : 입력으로 받은 시작점으로부터 시작 방향으로 길이가 1인 선분 긋기
1세대
:: 모든 점 : 0세대의 모든 점 + 0세대 끝점 기준으로 90도 시계방향 회전한 점
:: 끝점 : 시작점을 0세대 끝점을 기준으로 90도 시계방향 회전한 점
2세대
:: 모든 점 : 1세대 모든 점  + 1세대 끝점 기준으로 90도 시계방향 회전한 점
:: 끝점 : 시작점을 1세대 끝점을 기준으로 90도 시계방향 회전한 점

 

따라서! K세대 드래곤 커브의 점들은 이렇게 정리할 수 있다

모든 점 : K-1 세대의 모든 점 + K-1세대 끝점 기준으로 90도 시계방향 회전한 점
끝점 : 시작점을 K-1세대 끝점을 기준으로 90도 시계방향 회전한 점

 

1. 입력 받기

입력에서 들어온 정보 저장

드래곤 커브의 x,y 좌표 최대값이 100이기 때문에  좌표값을 저장하기 위해 101*101 배열을 생성 

public class Main {
	static int[] dy = {0,-1,0,1}; // 우상좌하
	static int[] dx = {1,0,-1,0}; // 우상좌하
	static int[][] data;
	static boolean[][] map; // 좌표값 저장
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		data = new int[N][4];
		map = new boolean[101][101]; // 좌표값 저장
		
		for(int i=0; i<N; i++) {
			StringTokenizer st = new StringTokenizer(br.readLine()," ");
			data[i][0] = Integer.parseInt(st.nextToken()); // 시작 x 좌표
			data[i][1] = Integer.parseInt(st.nextToken()); // 시작 y 좌표
			data[i][2] = Integer.parseInt(st.nextToken()); // 시작 방향
			data[i][3] = Integer.parseInt(st.nextToken()); // 세대
		}
	}
}

 

 

2. 드래곤 커브 그리기

세대가 증가할 때, 이전 세대의 정보가 필요하기 때문에 재귀로 구현

최종 세대까지 커브가 완성되면 드래곤 커브의 모든 좌표들을 저장하고 종료

 

커브 정보 저장

모든 점 : K-1 세대의 모든 점 + K-1세대 끝점 기준으로 90도 시계방향 회전한 점
끝점 : 시작점을 K-1세대 끝점을 기준으로 90도 시계방향 회전한 점

커브 정보는 이렇게 정리할 수 있기 때문에 모든 점을 저장할 부분과 끝점을 저장할 부분이 필요!

모든 점은 세대가 커질수록 점점 늘어나게 되기 때문에 ArrayList로 생성

class Curve {
	ArrayList<int[]> points = new ArrayList<>();
	int[] endpoint;
	
	Curve() {};
	
	Curve(int[] point, int[] end) {
		points.add(point);
		endpoint = end;
	}
	
	Curve(int[] point) {
		points.add(point);
	}
}

 

 

 

0세대 그리기

0세는 입력으로 받은 시작점으로부터 시작 방향으로 길이가 1인 선분 긋기

 

그외 세대 그리기

현재 세대의 커브를 그리려면 이전 세대의 정보가 필요하기 때문에 Curve[] curves를 매개변수로 넘겨서 세대별로 드래곤 커브의 정보를 저장 + 관리 했다.

 

1. 현재 세대의 인덱스로 Curve 객체를 생성

2. 이전 세대(cnt-1)의 점들을 현재 세대의 점들로 추가

3.  이전 세대 점들을 이전 세대 점들의 90도 회전해서 추가

 

📌 놓쳤던 부분!

회전을 할 때 회전 행렬을 사용했다. 이때 시계방향 반시계 방향에 따라 회전 행렬이 달라지는데 문제의 좌표평면에서 y축의 방향이 ⬇이기 때문에 y축의 방향이 ⬆였을 때 회전 행렬을 사용하려면 반시계 방향으로 회전을 해줘야 한다

 

한 세대의 커브 그리기가 끝나면 cnt+1을 통해 다음 세대를 그릴 수 있도록 했다.

 

 

커브 완성 후

커브가 완성 됐을 때, 마지막 세대는 이전 세대의 모든 점의 정보를 가지고 있기 때문에 마지막 세대 커브만 확인해 커브를 찍은 모든 좌표를 2차원 배열에 true로 표현

 

// index : data에서 몇 번째 정보인지 , cnt : 현재 몇 세대 커브인지, gen : 최종 세대 값, curves : 각 세대 커브 좌표
	static void drawCurve(int index, int cnt, int gen, Curve[] curves) {
		if(cnt == gen+1) {
			// 드래곤 커브 완성 후 긋기
			for(int i=0; i<curves[cnt-1].points.size(); i++) {
				int[] pos = curves[cnt-1].points.get(i);
				if(!map[pos[0]][pos[1]]) map[pos[0]][pos[1]] = true;
			}
			int[] end = curves[cnt-1].endpoint;
			map[end[0]][end[1]] = true;
			return;
		}
		
		if(cnt == 0) { // 0세대 만들기
			int d = data[index][2];
			int[] start = {data[index][0], data[index][1]};
			int[] end = {data[index][0] + dx[d], data[index][1] + dy[d]};
			curves[cnt] = new Curve(start, end);
			drawCurve(index, cnt+1, gen, curves);
		}
		else {
			curves[cnt] = new Curve();
			
			//이전 세대 점들을 현재 세대 점들로
			for(int i=0; i<curves[cnt-1].points.size(); i++) {
				int[] start = curves[cnt-1].points.get(i);
				curves[cnt].points.add(start);
			}
			curves[cnt].points.add(curves[cnt-1].endpoint); // 이전 세대 끝점도 현제 세대 점으로 추가
			
			// 이전 세대 점들(끝점 제외) 회전 시켜서  추가하기 - 시작점은 끝점으로 추가
			for(int i=0; i<curves[cnt-1].points.size(); i++) {
				int[] start = curves[cnt-1].points.get(i);
				int rotateX =  -1*(start[1] - curves[cnt-1].endpoint[1]) + curves[cnt-1].endpoint[0];
				int rotateY = start[0] - curves[cnt-1].endpoint[0] + curves[cnt-1].endpoint[1];
				if(i == 0) { // 시작점이면 끝점으로 추가하기
					curves[cnt].endpoint = new int[]{rotateX, rotateY};
				}
				else {
					curves[cnt].points.add(new int[]{rotateX, rotateY});
				}
			}
			
			//다음 세대 커브 진행
			drawCurve(index, cnt+1, gen, curves);
		}
	}

 

 

3. 정사각형 네 꼭짓점이 모두 드래곤 커브의 일부인 개수 찾기 

2차원 배열을 돌면서 [i, j] 를 왼쪽 상단의 점이라고 생각해  [i, j]를 기준으로 좌하단([i+1, j]), 우상단([i, j+1]), 좌하단([i+1, j+1]) 이 모두 true로 찍혀있다면 정사각형 네 꼭짓점이 모두 드래곤 커브라고 판단

// 정사각형 네 꼭짓점이 드래곤 커브인 것 구하기
int cnt =0;
for(int i=0; i<100; i++) {
	for(int j=0; j<100; j++) {
		if(map[i][j] && map[i+1][j] && map[i][j+1] && map[i+1][j+1]) cnt++;
	}
}

 

 

4. 전체 코드

import java.io.*;
import java.util.*;

class Curve {
	ArrayList<int[]> points = new ArrayList<>();
	int[] endpoint;
	
	Curve() {};
	
	Curve(int[] point, int[] end) {
		points.add(point);
		endpoint = end;
	}
	
	Curve(int[] point) {
		points.add(point);
	}
}

public class Main {
	static int[] dy = {0,-1,0,1}; // 우상좌하
	static int[] dx = {1,0,-1,0}; // 우상좌하
	static int[][] data;
	static boolean[][] map;
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		data = new int[N][4];
		map = new boolean[101][101];
		
		for(int i=0; i<N; i++) {
			StringTokenizer st = new StringTokenizer(br.readLine()," ");
			data[i][0] = Integer.parseInt(st.nextToken()); // 시작 x 좌표
			data[i][1] = Integer.parseInt(st.nextToken()); // 시작 y 좌표
			data[i][2] = Integer.parseInt(st.nextToken()); // 시작 방향
			data[i][3] = Integer.parseInt(st.nextToken()); // 세대
		}
		
		// 드래곤 커브 그리기
		for(int i=0; i<N; i++) {
			drawCurve(i, 0, data[i][3], new Curve[data[i][3]+1]);
		}
		
		// 정사각형 네 꼭짓점이 드래곤 커브인 것 구하기
		int cnt =0;
		for(int i=0; i<100; i++) {
			for(int j=0; j<100; j++) {
				if(map[i][j] && map[i+1][j] && map[i][j+1] && map[i+1][j+1]) cnt++;
			}
		}
		System.out.println(cnt);
	}
	
	// index : data에서 몇 번째 정보인지 , cnt : 현재 몇 세대 커브인지, gen : 최종 세대 값, curves : 각 세대 커브 좌표
	static void drawCurve(int index, int cnt, int gen, Curve[] curves) {
		if(cnt == gen+1) {
			// 드래곤 커브 완성 후 긋기
			for(int i=0; i<curves[cnt-1].points.size(); i++) {
				int[] pos = curves[cnt-1].points.get(i);
				if(!map[pos[0]][pos[1]]) map[pos[0]][pos[1]] = true;
			}
			int[] end = curves[cnt-1].endpoint;
			map[end[0]][end[1]] = true;
			return;
		}
		
		if(cnt == 0) { // 0세대 만들기
			int d = data[index][2];
			int[] start = {data[index][0], data[index][1]};
			int[] end = {data[index][0] + dx[d], data[index][1] + dy[d]};
			curves[cnt] = new Curve(start, end);
			drawCurve(index, cnt+1, gen, curves);
		}
		else {
			curves[cnt] = new Curve();
			
			//이전 세대 점들을 현재 세대 점들로
			for(int i=0; i<curves[cnt-1].points.size(); i++) {
				int[] start = curves[cnt-1].points.get(i);
				curves[cnt].points.add(start);
			}
			curves[cnt].points.add(curves[cnt-1].endpoint); // 이전 세대 끝점도 현제 세대 점으로 추가
			
			// 이전 세대 점들(끝점 제외) 회전 시켜서  추가하기 - 시작점은 끝점으로 추가
			for(int i=0; i<curves[cnt-1].points.size(); i++) {
				int[] start = curves[cnt-1].points.get(i);
				int rotateX =  -1*(start[1] - curves[cnt-1].endpoint[1]) + curves[cnt-1].endpoint[0];
				int rotateY = start[0] - curves[cnt-1].endpoint[0] + curves[cnt-1].endpoint[1];
				if(i == 0) { // 시작점이면 끝점으로 추가하기
					curves[cnt].endpoint = new int[]{rotateX, rotateY};
				}
				else {
					curves[cnt].points.add(new int[]{rotateX, rotateY});
				}
			}
			
			//다음 세대 커브 진행
			drawCurve(index, cnt+1, gen, curves);
		}
	}
}

 

 

5. 정리

좀 더 간단한 방법이 있을 것 같기도?

ArrayList에 점을 저장하지 않고 map에 바로 표시하는 방법도 있을 거 같기도?

 

 

어제 스터디를 하다가 더 좋은 방법을 공유 받았다!👇

• 드래곤 커브를 그리는 패턴을 찾고 
• 그 커브대로 방향을 저장
• 방향을 확인하며 정사각형 4개가 드래곤 커브인지 확인

[백준] 15685번: 드래곤 커브 문제 풀이